
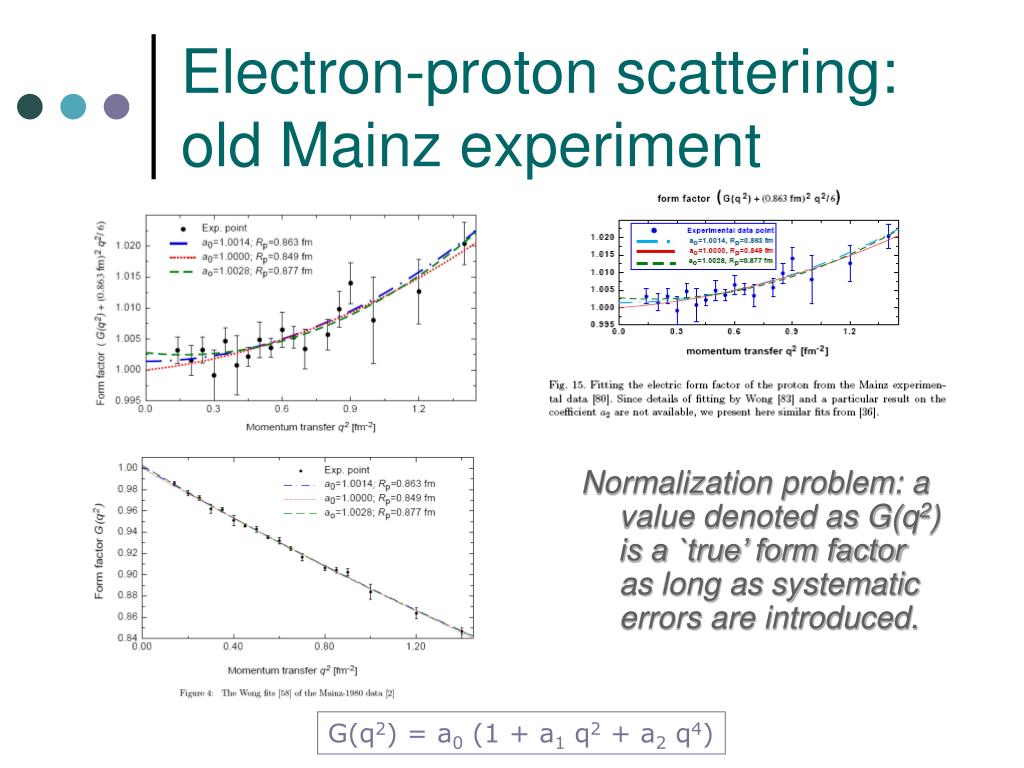
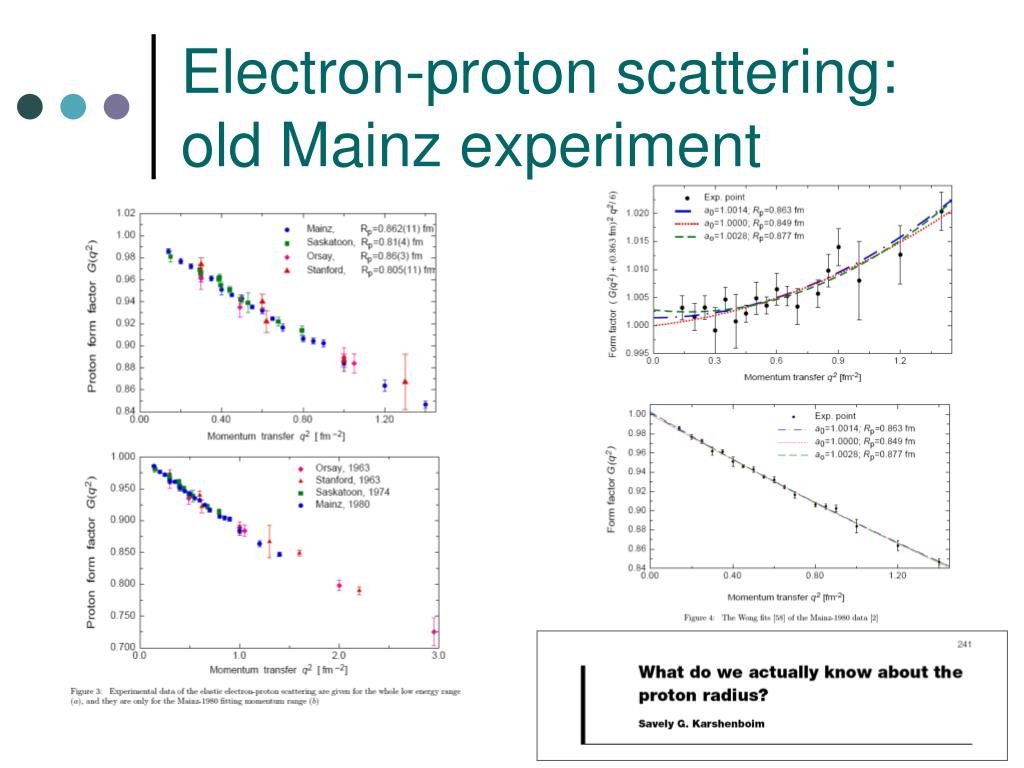
The proton Zemach radius, R p, is a fundamental parameter related to the spatial distribution of both the electric charge and the magnetic moment of the proton. One way to address the disagreements over the proton charge radius is to measure a different but complementary aspect of the proton electromagnetic structure. Discussions about the correctness of the theory, experiments, or the adequacy of the models are not leading to satisfactory explanations of this relevant discrepancy.
5 It is noteworthy that QED considerations show 6 that the electron scattering experiments and the atomic hydrogen spectroscopy determine the same radius. Specifically, a compilation of physical constants (CODATA) gives r p=0.8768(69)fm, 2 the Lamb shift of electronic hydrogen results in r p=0.883(14)fm, 3, 4 and electron scattering from hydrogen yields r p=0.895(18)fm. These earlier values come from three very different methods that are based mostly on electronic hydrogen data. 1 The reported value, r p=0.84184(67)fm, differs by 5 standard deviations from (and is a factor of 10 more precise than) previous determinations. (Muons are like electrons but 200 times heavier.) A recent spectroscopic study of muonic hydrogen resulted in a new measurement of the proton root mean square (rms) charge radius. Its value is used together with the Rydberg constant in the calculations of bound-state QED involving hydrogen atoms as well as muonic hydrogen atoms that have a muon orbiting the nucleus rather than the electron. The charge radius r p of the proton is a physical parameter that characterizes important aspects of the effective size of the proton.
Today, the interpretation of this data is only limited by the uncertainties in the size of the nucleus, which in the case of hydrogen is a single proton. However, these corrections have become important in recent high-precision measurements of transitions in the hydrogen atom, which are being performed to test quantum electrodynamics (QED) and to determine related fundamental constants. Consequently, the nuclear corrections to atomic energy levels are very tiny. The size of an atom's nucleus is roughly five orders of magnitude smaller than the size of the atom.


 0 kommentar(er)
0 kommentar(er)
